جدول جيب الظلال. الدوال المثلثية
في المقالة سوف نفهم تمامًا كيف يبدو الأمر جدول القيم المثلثية، الجيب، وجيب التمام، والظل، وظل التمام. دعونا نفكر في المعنى الأساسي للدوال المثلثية، من زاوية 0،30،45،60،90،...،360 درجة. ولنرى كيفية استخدام هذه الجداول في حساب قيم الدوال المثلثية.
أولا دعونا ننظر جدول جيب التمام، الجيب، الظل وظل التماممن زاوية 0، 30، 45، 60، 90،... درجة. يتيح لنا تعريف هذه الكميات تحديد قيمة دوال الزوايا 0 و 90 درجة:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0، ظل التمام من 00 سيكون غير محدد
sin 90 0 = 1، cos 90 0 =0، ctg90 0 = 0، الظل من 90 0 سيكون غير مؤكد
إذا كنت تأخذ مثلثات قائمة زواياها من 30 إلى 90 درجة. نحن نحصل:
جا 30 0 = 1/2، جتا 30 = √3/2، ظا 30 0 = √3/3، جتا 30 = √3
جا 45 0 = √2/2, جتا 0 45 = √2/2, ظا 45 0 = 1, جتا 45 0 = 1
sin 60 0 = √3/2, cos 60 = 1/2, tg 60 0 =√3, cot 60 0 = √3/3
دعونا نمثل جميع القيم التي تم الحصول عليها في النموذج الجدول المثلثي:
جدول الجيب وجيب التمام والظل وظل التمام!
إذا استخدمنا صيغة التخفيض، فإن جدولنا سيزيد بإضافة قيم للزوايا حتى 360 درجة. سوف تبدو مثل:

أيضًا، بناءً على خصائص الدورية، يمكن زيادة الجدول إذا استبدلنا الزوايا بـ 0 0 +360 0 *z .... 330 0 +360 0 *z، حيث z عدد صحيح. من الممكن في هذا الجدول حساب قيمة جميع الزوايا المقابلة للنقاط الموجودة في دائرة واحدة.
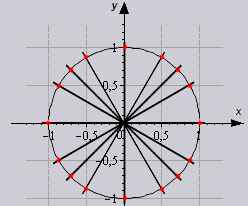
دعونا نلقي نظرة على كيفية استخدام الجدول في الحل.
كل شيء بسيط جدا. نظرًا لأن القيمة التي نحتاجها تقع عند نقطة تقاطع الخلايا التي نحتاجها. على سبيل المثال، خذ جتا زاوية قياسها 60 درجة، سيبدو في الجدول كما يلي:

في الجدول النهائي للقيم الرئيسية للدوال المثلثية، نسير بنفس الطريقة. لكن في هذا الجدول من الممكن معرفة مقدار المماس من زاوية 1020 درجة، فهو = -√3 لنتحقق من 1020 0 = 300 0 +360 0 *2. دعونا نجدها باستخدام الجدول.

طاولة براديس. لجيب التمام وجيب التمام والظل وظل التمام.
تنقسم جداول براديس إلى عدة أجزاء، تتكون من جداول جيب التمام والجيب والظل وظل التمام - وهي مقسمة إلى جزأين (tg من الزوايا حتى 90 درجة وctg من الزوايا الصغيرة).
جيب وجيب التمام


tg للزاوية تبدأ من 00 وتنتهي بـ 760، ctg للزاوية تبدأ بـ 140 وتنتهي بـ 900.
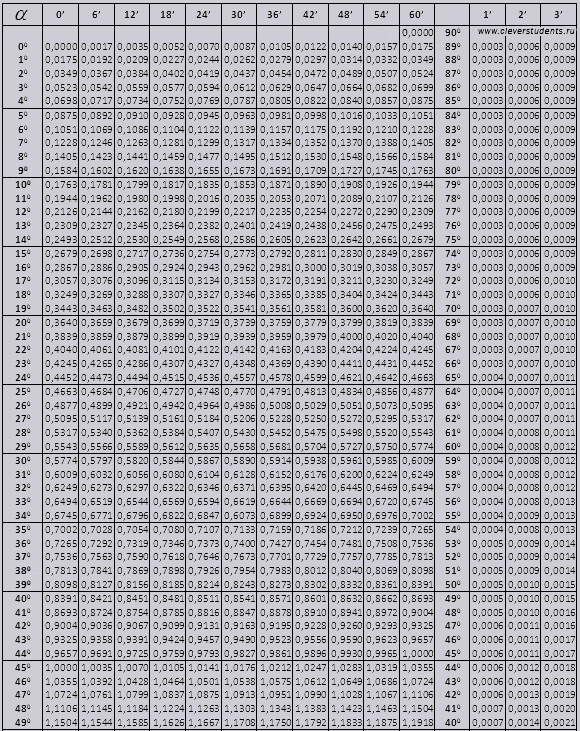

Tg ما يصل إلى 900 وctg من الزوايا الصغيرة.
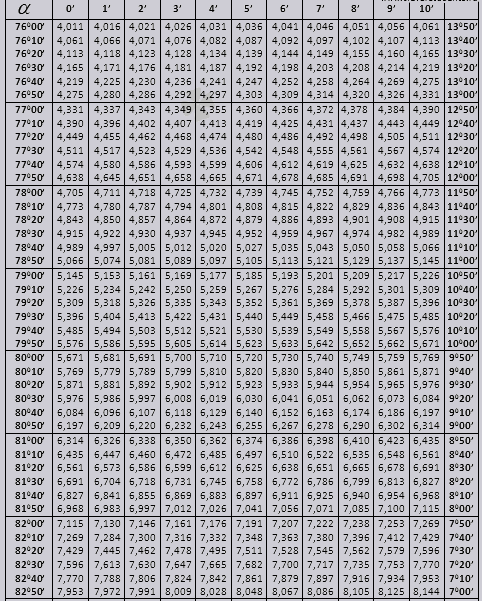
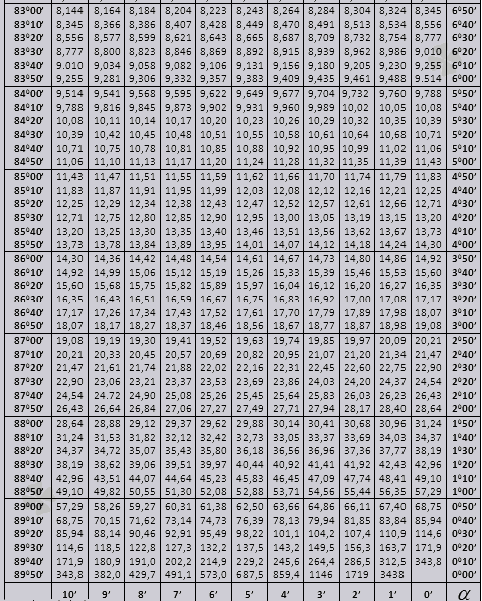
دعونا نتعرف على كيفية استخدام جداول Bradis في حل المشكلات.
لنجد التعيين sin (التعيين في العمود الموجود على الحافة اليسرى) 42 دقيقة (التعيين موجود في السطر العلوي). وبالتقاطع نبحث عن التسمية وهي = 0.3040.
تتم الإشارة إلى قيم الدقائق بفاصل زمني مدته ست دقائق، ماذا نفعل إذا كانت القيمة التي نحتاجها تقع بالضبط ضمن هذا الفاصل الزمني. لنأخذ 44 دقيقة، ولكن هناك 42 دقيقة فقط في الجدول. نأخذ 42 كأساس ونستخدم الأعمدة الإضافية على الجانب الأيمن، ونأخذ التعديل الثاني ونضيفه إلى 0.3040 + 0.0006 نحصل على 0.3046.
مع sin 47 دقيقة، نأخذ 48 دقيقة كأساس ونطرح منها تصحيحًا واحدًا، أي 0.3057 - 0.0003 = 0.3054
عند حساب cos، فإننا نعمل بشكل مشابه لـ sin، فقط نأخذ الصف السفلي من الجدول كأساس. على سبيل المثال cos 20 0 = 0.9397
قيم زاوية tg حتى 90 0 و cot زاوية صغيرة صحيحة ولا يوجد بها أي تصحيحات. على سبيل المثال، أوجد tg 78 0 37min = 4.967 
وctg 20 0 13 دقيقة = 25.83 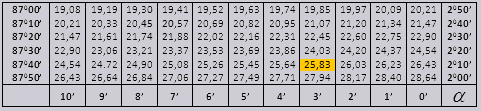
حسنًا، لقد ألقينا نظرة على الجداول المثلثية الأساسية. نأمل أن تكون هذه المعلومات مفيدة للغاية بالنسبة لك. إذا كان لديك أي أسئلة حول الجداول، تأكد من كتابتها في التعليقات!
ملاحظة: مصدات الحائط عبارة عن لوح ممتص للصدمات لحماية الجدران. اتبع الرابط مصدات الحائط بدون إطار (http://www.spi-polymer.ru/otboyniki/) واكتشف المزيد.
انتباه!
هناك اضافية
المواد في القسم الخاص 555.
بالنسبة لأولئك الذين هم "ليسوا جدا..."
ولأولئك الذين "كثيرا ...")
أولاً، اسمحوا لي أن أذكرك باستنتاج بسيط ولكنه مفيد للغاية من الدرس "ما هو الجيب وجيب التمام؟ ما هو الظل وظل التمام؟"
هذا هو الإخراج:
يرتبط جيب التمام وجيب التمام والظل وظل التمام ارتباطًا وثيقًا بزواياهم. نحن نعرف شيئًا واحدًا، مما يعني أننا نعرف شيئًا آخر.
بمعنى آخر، كل زاوية لها جيب التمام وجيب التمام الثابت الخاص بها. وكل شخص تقريبًا لديه ظل التمام وظل التمام الخاص به. لماذا بالكاد؟المزيد عن هذا أدناه.
هذه المعرفة تساعد كثيرا في دراستك! هناك الكثير من المهام التي تحتاج فيها إلى الانتقال من الجيوب إلى الزوايا والعكس. لهذا هناك جدول الجيوب.وبالمثل، بالنسبة للمهام ذات جيب التمام - جدول جيب التمام.وكما كنت قد خمنت، هناك جدول الظلو جدول ظل التمام.)
الجداول مختلفة. الطويلة، حيث يمكنك أن ترى ما يساوي، على سبيل المثال، sin37°6’. نفتح جداول براديس ونبحث عن زاوية مقدارها سبعة وثلاثون درجة وست دقائق ونرى القيمة 0.6032. من الواضح أنه ليست هناك حاجة على الإطلاق لتذكر هذا الرقم (وآلاف قيم الجدول الأخرى).
في الواقع، في عصرنا، ليست هناك حاجة حقًا إلى جداول طويلة من جيب التمام، وجيب التمام، والظلال، وظل التمام. آلة حاسبة واحدة جيدة تحل محلها بالكامل. لكن لا يضر معرفة وجود مثل هذه الجداول. لسعة الاطلاع العامة.)
ولماذا هذا الدرس إذن؟! - أنت تسأل.
لكن لماذا. من بين العدد اللانهائي من الزوايا هناك خاص،والتي يجب أن تعرف عنها الجميع. جميع الهندسة المدرسية وعلم المثلثات مبنية على هذه الزوايا. هذا نوع من "جدول الضرب" في علم المثلثات. إذا كنت لا تعرف ما هي قيمة الخطيئة 50 درجة، على سبيل المثال، فلن يحكم عليك أحد.) ولكن إذا كنت لا تعرف ما هي قيمة الخطيئة 30 درجة، فكن مستعدًا للحصول على جائزتين بجدارة...
هذه خاصالزوايا هي أيضا جيدة جدا. عادة ما تقدم الكتب المدرسية الحفظ جدول الجيب وجدول جيب التماملسبعة عشر زاوية. وبالطبع، جدول الظل وجدول ظل التماملنفس الزوايا السبع عشرة... أي: يقترح أن نتذكر 68 القيم. وهي، بالمناسبة، متشابهة جدًا مع بعضها البعض، تكرر نفسها بين الحين والآخر وتغير الإشارات. بالنسبة لشخص ليس لديه ذاكرة بصرية كاملة، فهذه مهمة كبيرة...)
سنتخذ طريقًا مختلفًا. دعونا نستبدل الحفظ عن ظهر قلب بالمنطق والإبداع. ثم سيتعين علينا حفظ 3 (ثلاثة!) قيم لجدول الجيب وجدول جيب التمام. و3 (ثلاثة!) قيم لجدول الظلال وجدول ظل التمام. هذا كل شئ. ست قيم أسهل في التذكر من 68، على ما يبدو لي...)
سوف نحصل على جميع القيم الضرورية الأخرى من هذه القيم الستة باستخدام ورقة غش قانونية قوية - الدائرة المثلثية. إذا لم تكن قد درست هذا الموضوع، فاتبع الرابط، ولا تكن كسولاً. هذه الدائرة ليست ضرورية لهذا الدرس فقط. إنه لا يمكن الاستغناء عنه لجميع علم المثلثات في وقت واحد. عدم استخدام مثل هذه الأداة هو مجرد خطيئة! انت لا تريد؟ هذا هو عملك حفظ جدول الجيوب. جدول جيب التمام. جدول الظلال. جدول ظل التمام.جميع القيم 68 لمجموعة متنوعة من الزوايا.)
لذلك، دعونا نبدأ. أولاً، دعونا نقسم كل هذه الزوايا الخاصة إلى ثلاث مجموعات.
المجموعة الأولى من الزوايا.
دعونا نفكر في المجموعة الأولى سبعة عشر زاوية خاص. هذه هي 5 زوايا: 0 درجة، 90 درجة، 180 درجة، 270 درجة، 360 درجة.
هذا ما يبدو عليه جدول الجيب وجيب التمام والظل وظل التمام لهذه الزوايا:
زاوية س
|
0 |
90 |
180 |
270 |
360 |
زاوية س
|
0 |
||||
الخطيئة س |
0 |
1 |
0 |
-1 |
0 |
كوس س |
1 |
0 |
-1 |
0 |
1 |
تيراغرام س |
0 |
اسم |
0 |
اسم |
0 |
سي تي جي × |
اسم |
0 |
اسم |
0 |
اسم |
ومن أراد أن يتذكر فليتذكر. لكنني سأقول على الفور أن كل هذه الآحاد والأصفار مرتبكة جدًا في رأسي. أقوى بكثير مما تريد.) لذلك نقوم بتشغيل المنطق والدائرة المثلثية.
نرسم دائرة ونحدد عليها نفس الزوايا: 0°، 90°، 180°، 270°، 360°. قمت بتمييز هذه الزوايا بنقاط حمراء:

من الواضح على الفور ما هو المميز في هذه الزوايا. نعم! هذه هي الزوايا التي تسقط بالضبط على محور الإحداثيات!في الواقع، لهذا السبب يرتبك الناس... لكننا لن نرتبك. دعونا نتعرف على كيفية العثور على الدوال المثلثية لهذه الزوايا دون حفظ الكثير.
بالمناسبة، موضع الزاوية هو 0 درجة يتزامن تمامامع وضع زاوية 360 درجة. وهذا يعني أن الجيب وجيب التمام والظل لهذه الزوايا هي نفسها تمامًا. لقد حددت زاوية 360 درجة لإكمال الدائرة.
لنفترض، في البيئة الصعبة والمجهدة لامتحان الدولة الموحدة، أنك شككت بطريقة أو بأخرى... ما هو جيب الزاوية 0 درجة؟ يبدو وكأنه صفر... وماذا لو كان واحداً؟! الحفظ الميكانيكي هو شيء من هذا القبيل. وفي الظروف القاسية تبدأ الشكوك تنخر...)
اهدأ، فقط اهدأ!) سأخبرك بأسلوب عملي سيمنحك إجابة صحيحة بنسبة 100% ويزيل كل الشكوك تمامًا.
على سبيل المثال، دعونا نتعرف على كيفية تحديد جيب الزاوية 0 درجة بشكل واضح وموثوق. وفي الوقت نفسه، جيب التمام 0. ومن الغريب أن الناس غالبًا ما يشعرون بالارتباك في هذه القيم.
للقيام بذلك، ارسم على دائرة اِعتِباطِيّركن X. وفي الربع الأول كانت قريبة من 0 درجة. دعونا نحدد جيب وجيب التمام لهذه الزاوية على المحاور X،كل شيء على ما يرام. مثله:
والآن - انتبه! دعونا نقلل الزاوية X، اجعل الجانب المتحرك أقرب إلى المحور أوه. حرك مؤشر الماوس فوق الصورة (أو اضغط على الصورة على جهازك اللوحي) وسترى كل شيء.
الآن دعونا ننتقل إلى المنطق الأولي!فلننظر ونفكر: كيف يتصرف sinx عندما تتناقص الزاوية x؟ عندما تقترب الزاوية من الصفر؟انها تتقلص! والكوسكس يزيد!يبقى أن نعرف ماذا سيحدث للجيب عندما تنهار الزاوية تمامًا؟ متى يستقر الضلع المتحرك للزاوية (النقطة A) على المحور OX وتصبح الزاوية صفراً؟ ومن الواضح أن جيب الزاوية سوف يذهب إلى الصفر. وسيزداد جيب التمام إلى... إلى... ما طول الضلع المتحرك للزاوية (نصف قطر الدائرة المثلثية)؟ واحد!
هنا هو الجواب. جيب تمام 0 درجة يساوي 0. جيب تمام 0 درجة يساوي 1. حديد تمامًا وبدون أي شك!) ببساطة لأنه بخلاف ذلك لا يمكن أن تكون.
بنفس الطريقة تمامًا، يمكنك معرفة (أو توضيح) جيب الزاوية 270 درجة، على سبيل المثال. أو جيب التمام 180. ارسم دائرة، اِعتِباطِيّزاوية في الربع بجوار محور الإحداثيات الذي يهمنا، حرك جانب الزاوية عقليًا وافهم ما سيصبح عليه الجيب وجيب التمام عندما يقع جانب الزاوية على المحور. هذا كل شئ.
كما ترون، ليست هناك حاجة لحفظ أي شيء لهذه المجموعة من الزوايا. ليست هناك حاجة هنا جدول الجيوب...نعم و جدول جيب التمام- أيضًا.) بالمناسبة، بعد عدة استخدامات للدائرة المثلثية، سيتم تذكر كل هذه القيم من تلقاء نفسها. وإذا نسوا رسمت دائرة في 5 ثواني ووضحتها. أسهل بكثير من الاتصال بصديق من المرحاض والمخاطرة بشهادتك، أليس كذلك؟)
أما بالنسبة للظل وظل التمام، فكل شيء هو نفسه. نرسم خط ظل (ظل التمام) على الدائرة - وكل شيء مرئي على الفور. حيث تساوي الصفر، وحيث لا وجود لها. ماذا، ألا تعرف عن خطوط المماس وظل التمام؟ هذا أمر محزن، ولكن يمكن إصلاحه.) قمنا بزيارة القسم 555 ظل وظل التمام على الدائرة المثلثية - ولا توجد مشاكل!
إذا كنت قد اكتشفت كيفية تحديد جيب التمام وجيب التمام والظل وظل التمام لهذه الزوايا الخمس بوضوح، تهانينا! فقط في حالة إبلاغك أنه يمكنك الآن تحديد الوظائف أي الزوايا الساقطة على المحاور.وهذه هي 450 درجة، و540 درجة، و1800 درجة، وعدد لا حصر له من الآخرين...) لقد حسبت (بشكل صحيح!) الزاوية الموجودة على الدائرة - ولا توجد مشاكل في الوظائف.
ولكن بالتحديد مع قياس الزوايا تحدث المشاكل والأخطاء... كيفية تجنبها مكتوبة في الدرس: كيفية رسم (عد) أي زاوية على دائرة مثلثية بالدرجات. ابتدائية ولكنها مفيدة جدًا في مكافحة الأخطاء.)
إليك درسًا: كيفية رسم (قياس) أي زاوية على دائرة مثلثية بالراديان - سيكون الأمر أكثر روعة. من حيث الإمكانيات. لنفترض أننا حددنا على أي من أنصاف المحاور الأربعة تقع الزاوية
يمكنك القيام بذلك في بضع ثوان. أنا لا أمزح! فقط في بضع ثوان. حسنًا، بالطبع، ليس فقط 345 بي...) و121 و16 و-1345. أي معامل عدد صحيح مناسب للإجابة الفورية.
وإذا الزاوية
فقط فكر! يتم الحصول على الإجابة الصحيحة خلال 10 ثوانٍ لأي قيمة كسرية للراديان بمقامها اثنان.
في الواقع، هذا هو الشيء الجيد في الدائرة المثلثية. لأن القدرة على العمل مع بعضالزوايا التي تتوسع إليها تلقائيًا مجموعة لا نهائيةزوايا
إذن، نكون قد فرزنا خمس زوايا من سبعة عشر.
المجموعة الثانية من الزوايا.
المجموعة التالية من الزوايا هي الزوايا 30° و45° و60°. لماذا بالضبط هذه، وليس، على سبيل المثال، 20 و 50 و 80؟ نعم، بطريقة ما اتضح الأمر بهذه الطريقة... تاريخيًا.) بعد ذلك سنرى لماذا هذه الزوايا جيدة.
يبدو جدول جيب التمام وظل التمام لهذه الزوايا كما يلي:
زاوية س
|
0 |
30 |
45 |
60 |
90 |
زاوية س
|
0 |
||||
الخطيئة س |
0 |
1 |
|||
كوس س |
1 |
0 |
|||
تيراغرام س |
0 |
1 |
اسم |
||
سي تي جي × |
اسم |
1 |
0 |
لقد تركت القيمتين 0° و 90° من الجدول السابق لتكتمل الصورة.) لكي ترى أن هذه الزوايا تقع في الربع الأول وتزداد. من 0 إلى 90. سيكون هذا مفيدًا لنا لاحقًا.
يجب تذكر قيم الجدول للزوايا 30 درجة و 45 درجة و 60 درجة. احفظها إذا أردت. ولكن هنا أيضًا هناك فرصة لجعل حياتك أسهل.) انتبه إلى ذلك قيم الجدول الجيبيةهذه الزوايا. وقارن مع قيم جدول جيب التمام...
نعم! هم نفس!مجرد ترتيب في ترتيب عكسي. زيادة الزوايا (0، 30، 45، 60، 90) - وقيم الجيب يزيدمن 0 إلى 1. يمكنك التحقق باستخدام الآلة الحاسبة. وقيم جيب التمام هي تتناقصمن 1 إلى الصفر. علاوة على ذلك، القيم نفسها نفس.بالنسبة للزوايا 20، 50، 80 هذا لن ينجح...
وهذا هو الاستنتاج المفيد. يكفي أن نتعلم ثلاثةقيم الزوايا 30، 45، 60 درجة. وتذكر أنهم يزيدون على جيب التمام وينقصون على جيب التمام. نحو جيب التمام.) يلتقيان في منتصف الطريق (45 درجة)، أي أن جيب 45 درجة يساوي جيب تمام 45 درجة. ومن ثم يتباعدان مرة أخرى... يمكن تعلم ثلاثة معانٍ، أليس كذلك؟
مع الظلال - ظل التمام، الصورة هي نفسها تمامًا. واحد لواحد. فقط المعاني مختلفة. هذه القيم (ثلاثة أخرى!) تحتاج أيضًا إلى تعلمها.
حسنا، تقريبا كل الحفظ قد انتهى. لقد فهمت (نأمل) كيفية تحديد قيم الزوايا الخمس الواقعة على المحور وتعلمت قيم الزوايا 30، 45، 60 درجة. المجموع 8.
يبقى التعامل مع المجموعة الأخيرة المكونة من 9 زوايا.
وهذه هي الزوايا:
120 درجة؛ 135 درجة؛ 150 درجة؛ 210 درجة؛ 225 درجة؛ 240 درجة؛ 300 درجة؛ 315 درجة؛ 330 درجة. بالنسبة لهذه الزوايا، عليك أن تعرف جدول الجيب، وجدول جيب التمام، وما إلى ذلك.
كابوس أليس كذلك؟)
وإذا أضفت زوايا هنا، مثل: 405 درجة، أو 600 درجة، أو 3000 درجة والعديد والعديد من الزوايا المتساوية في الجمال؟)
أو الزوايا بالراديان؟ على سبيل المثال، حول الزوايا:

وغيرها الكثير يجب أن تعرف الجميع.
الشيء المضحك هو معرفة هذا الجميع - مستحيل من حيث المبدأ.إذا كنت تستخدم الذاكرة الميكانيكية.
وهو أمر سهل للغاية، بل إنه في واقع الأمر أمر بدائي - إذا كنت تستخدم دائرة مثلثية. بمجرد أن تتقن التعامل مع الدائرة المثلثية، يمكن بسهولة وبطريقة أنيقة اختزال كل تلك الزوايا المخيفة بالدرجات إلى الزوايا القديمة الجيدة:
بالمناسبة، لدي موقعين أكثر إثارة للاهتمام بالنسبة لك.)
يمكنك التدرب على حل الأمثلة ومعرفة مستواك. الاختبار مع التحقق الفوري. دعونا نتعلم - باهتمام!)
يمكنك التعرف على الوظائف والمشتقات.
في القرن الخامس قبل الميلاد، صاغ الفيلسوف اليوناني القديم زينون الإيلي مفارقاته الشهيرة، وأشهرها مفارقات “أخيل والسلحفاة”. وهنا ما يبدو وكأنه:لنفترض أن أخيل يجري أسرع بعشر مرات من السلحفاة ويتخلف عنها بألف خطوة. خلال الوقت الذي يستغرقه أخيل في قطع هذه المسافة، ستزحف السلحفاة مائة خطوة في نفس الاتجاه. فعندما يركض أخيل مائة خطوة، تزحف السلحفاة عشر خطوات أخرى، وهكذا. ستستمر العملية إلى ما لا نهاية، ولن يتمكن أخيل من اللحاق بالسلحفاة أبدًا.
أصبح هذا المنطق بمثابة صدمة منطقية لجميع الأجيال اللاحقة. أرسطو، ديوجين، كانط، هيجل، هيلبرت... كلهم اعتبروا معضلة زينون بطريقة أو بأخرى. وكانت الصدمة قوية لدرجة " ... تستمر المناقشات حتى يومنا هذا، ولم يتمكن المجتمع العلمي بعد من التوصل إلى رأي مشترك حول جوهر المفارقات ... وقد شارك التحليل الرياضي، ونظرية المجموعات، والمناهج الفيزيائية والفلسفية الجديدة في دراسة هذه القضية؛ ; ولم يصبح أي منها حلاً مقبولاً بشكل عام للمشكلة ..."[ويكيبيديا، "أبوريا زينو". الجميع يفهم أنه يتم خداعهم، ولكن لا أحد يفهم ما يتكون الخداع.
من وجهة نظر رياضية، أظهر زينون في كتابه المحرج بوضوح الانتقال من الكمية إلى . يتضمن هذا الانتقال التطبيق بدلاً من التطبيقات الدائمة. بقدر ما أفهم، فإن الجهاز الرياضي لاستخدام وحدات القياس المتغيرة إما لم يتم تطويره بعد، أو لم يتم تطبيقه على مفارقة زينون. إن تطبيق منطقنا المعتاد يقودنا إلى الفخ. نحن، بسبب الجمود في التفكير، نطبق وحدات زمنية ثابتة على القيمة المتبادلة. من الناحية الفيزيائية، يبدو أن الزمن يتباطأ حتى يتوقف تمامًا في اللحظة التي يلحق فيها أخيل بالسلحفاة. إذا توقف الزمن، لن يتمكن أخيل من تجاوز السلحفاة.
إذا قلبنا منطقنا المعتاد، فإن كل شيء يقع في مكانه. يجري أخيل بسرعة ثابتة. كل جزء لاحق من طريقه أقصر بعشر مرات من الجزء السابق. وعليه فإن الوقت المستغرق في التغلب عليها أقل بعشر مرات من الوقت السابق. ولو طبقنا مفهوم "اللانهاية" في هذه الحالة، لصح أن نقول "أخيل سوف يلحق بالسلحفاة بسرعة لا متناهية".
كيفية تجنب هذا الفخ المنطقي؟ ابق في وحدات زمنية ثابتة ولا تتحول إلى وحدات متبادلة. في لغة زينو يبدو الأمر كما يلي:
في الوقت الذي يستغرقه أخيل في الجري ألف خطوة، ستزحف السلحفاة مائة خطوة في نفس الاتجاه. خلال الفترة الزمنية التالية المساوية للأولى، سيجري أخيل ألف خطوة أخرى، وستزحف السلحفاة مائة خطوة. والآن يتقدم أخيل على السلحفاة بثمانمائة خطوة.
يصف هذا النهج الواقع بشكل مناسب دون أي مفارقات منطقية. ولكن هذا ليس الحل الكامل للمشكلة. إن عبارة أينشتاين حول عدم مقاومة سرعة الضوء تشبه إلى حد كبير مقولة زينو "أخيل والسلحفاة". لا يزال يتعين علينا دراسة هذه المشكلة وإعادة التفكير فيها وحلها. ويجب البحث عن الحل ليس بأعداد كبيرة بلا حدود، بل بوحدات القياس.
تحكي aporia أخرى مثيرة للاهتمام لزينو عن سهم طائر:
السهم الطائر لا يتحرك، لأنه في كل لحظة من الزمن يكون ساكنًا، وبما أنه ساكن في كل لحظة من الزمن، فهو ساكن دائمًا.
في هذه المعضلة، يتم التغلب على المفارقة المنطقية بكل بساطة - يكفي توضيح أنه في كل لحظة من الزمن يكون السهم الطائر في حالة سكون عند نقاط مختلفة في الفضاء، وهو في الواقع حركة. هناك نقطة أخرى يجب الإشارة إليها هنا. من خلال صورة واحدة لسيارة على الطريق، من المستحيل تحديد حقيقة حركتها أو المسافة إليها. لتحديد ما إذا كانت السيارة تتحرك، تحتاج إلى صورتين تم التقاطهما من نفس النقطة في نقاط زمنية مختلفة، لكن لا يمكنك تحديد المسافة منهما. لتحديد المسافة إلى السيارة، تحتاج إلى صورتين تم التقاطهما من نقاط مختلفة في الفضاء في وقت واحد، ولكن من المستحيل تحديد حقيقة الحركة (بالطبع، لا تزال بحاجة إلى بيانات إضافية للحسابات، وسوف يساعدك علم المثلثات ). وما أريد أن ألفت انتباهًا خاصًا إليه هو أن النقطتين في الزمن ونقطتين في المكان هما شيئان مختلفان ولا ينبغي الخلط بينهما، لأنهما يوفران فرصًا مختلفة للبحث.
الأربعاء 4 يوليو 2018
تم وصف الاختلافات بين المجموعة والمجموعات المتعددة بشكل جيد للغاية على ويكيبيديا. دعنا نرى.
كما ترون، "لا يمكن أن يكون هناك عنصرين متطابقين في مجموعة"، ولكن إذا كان هناك عناصر متطابقة في مجموعة، فإن هذه المجموعة تسمى "مجموعة متعددة". لن تفهم الكائنات العاقلة مثل هذا المنطق السخيف. وهذا هو مستوى الببغاوات الناطقة والقردة المدربة، التي لا ذكاء لها من كلمة "تماماً". يعمل علماء الرياضيات كمدربين عاديين، ويبشروننا بأفكارهم السخيفة.
في يوم من الأيام، كان المهندسون الذين بنوا الجسر في قارب تحت الجسر أثناء اختبار الجسر. وإذا انهار الجسر مات المهندس المتوسط تحت ركام خلقه. وإذا كان الجسر قادرا على تحمل الأحمال، فقد قام المهندس الموهوب ببناء جسور أخرى.
بغض النظر عن مدى إخفاء علماء الرياضيات وراء عبارة "اهتم بي، أنا في المنزل"، أو بالأحرى، "الرياضيات تدرس المفاهيم المجردة"، هناك حبل سري واحد يربطهم بشكل لا ينفصم بالواقع. هذا الحبل السري هو المال. دعونا نطبق نظرية المجموعات الرياضية على علماء الرياضيات أنفسهم.
لقد درسنا الرياضيات جيدًا ونحن الآن نجلس عند ماكينة تسجيل المدفوعات النقدية ونوزع الرواتب. لذلك يأتي إلينا عالم الرياضيات من أجل ماله. نحسب له المبلغ بالكامل ونضعه على طاولتنا في أكوام مختلفة، حيث نضع فيها أوراقًا نقدية من نفس الفئة. ثم نأخذ فاتورة واحدة من كل كومة ونعطي عالم الرياضيات "مجموعة الراتب الحسابي". دعونا نوضح لعالم الرياضيات أنه لن يحصل على الأوراق النقدية المتبقية إلا عندما يثبت أن المجموعة التي لا تحتوي على عناصر متماثلة لا تساوي مجموعة ذات عناصر متطابقة. هنا يبدا المرح.
بادئ ذي بدء، سيعمل منطق النواب: "يمكن تطبيق هذا على الآخرين، ولكن ليس علي!" ثم سيبدأون في طمأنتنا بأن الأوراق النقدية من نفس الفئة لها أرقام فواتير مختلفة، مما يعني أنه لا يمكن اعتبارها نفس العناصر. حسنًا، لنحسب الرواتب بالعملات المعدنية - لا توجد أرقام على العملات المعدنية. هنا سيبدأ عالم الرياضيات في تذكر الفيزياء بشكل محموم: العملات المعدنية المختلفة تحتوي على كميات مختلفة من الأوساخ، والتركيب البلوري وترتيب الذرات فريد لكل عملة...
والآن لدي السؤال الأكثر إثارة للاهتمام: أين هو الخط الذي تتحول بعده عناصر المجموعة المتعددة إلى عناصر مجموعة والعكس صحيح؟ مثل هذا الخط غير موجود - كل شيء يقرره الشامان، والعلم ليس قريبًا حتى من الكذب هنا.
انظر هنا. نختار ملاعب كرة القدم بنفس مساحة الملعب. مساحات الحقول هي نفسها - مما يعني أن لدينا مجموعة متعددة. لكن إذا نظرنا إلى أسماء هذه الملاعب نفسها، فسنحصل على الكثير منها، لأن الأسماء مختلفة. كما ترون، نفس مجموعة العناصر هي مجموعة ومتعددة. ايهم صحيح؟ وهنا يقوم عالم الرياضيات الشامان الحاد بسحب الآس من الأوراق الرابحة من جعبته ويبدأ في إخبارنا إما عن مجموعة أو مجموعة متعددة. وفي كل الأحوال سيقنعنا بأنه على حق.
لفهم كيفية عمل الشامان الحديثين مع نظرية المجموعات، وربطها بالواقع، يكفي الإجابة على سؤال واحد: كيف تختلف عناصر مجموعة واحدة عن عناصر مجموعة أخرى؟ سأريكم، دون أي عبارة "لا يمكن تصورها كوحدة واحدة" أو "لا يمكن تصورها ككل واحد".
الأحد 18 مارس 2018
مجموع أرقام الرقم هو رقصة الشامان مع الدف، والتي لا علاقة لها بالرياضيات. نعم، في دروس الرياضيات، يتم تعليمنا كيفية العثور على مجموع أرقام الرقم واستخدامها، ولكن هذا هو السبب في أنهم شامان، لتعليم أحفادهم مهاراتهم وحكمتهم، وإلا فإن الشامان سوف يموتون ببساطة.
هل تحتاج إلى دليل؟ افتح ويكيبيديا وحاول العثور على صفحة "مجموع أرقام الرقم". هي غير موجودة. لا توجد صيغة في الرياضيات يمكن استخدامها لإيجاد مجموع أرقام أي رقم. بعد كل شيء، الأرقام هي رموز رسومية نكتب بها الأرقام، وفي لغة الرياضيات تبدو المهمة كما يلي: "ابحث عن مجموع الرموز الرسومية التي تمثل أي رقم". لا يستطيع علماء الرياضيات حل هذه المشكلة، لكن الشامان يمكنهم حلها بسهولة.
دعونا نكتشف ماذا وكيف نفعل للعثور على مجموع أرقام رقم معين. إذن، دعونا نحصل على الرقم 12345. ما الذي يجب فعله لإيجاد مجموع أرقام هذا الرقم؟ دعونا نفكر في جميع الخطوات بالترتيب.
1. اكتب الرقم على قطعة من الورق. ماذا فعلنا؟ لقد قمنا بتحويل الرقم إلى رمز رقم رسومي. هذه ليست عملية رياضية.
2. نقوم بقص الصورة الناتجة إلى عدة صور تحتوي على أرقام فردية. إن قطع الصورة ليس عملية رياضية.
3. تحويل الرموز الرسومية الفردية إلى أرقام. هذه ليست عملية رياضية.
4. أضف الأرقام الناتجة. الآن هذه هي الرياضيات.
مجموع أرقام الرقم 12345 هو 15. هذه هي "دورات القطع والخياطة" التي يدرسها الشامان والتي يستخدمها علماء الرياضيات. ولكن هذا ليس كل شيء.
من وجهة نظر رياضية، لا يهم في أي نظام أرقام نكتب رقمًا. لذا، في أنظمة الأرقام المختلفة، سيكون مجموع أرقام نفس الرقم مختلفًا. في الرياضيات، يُشار إلى نظام الأرقام كحرف منخفض على يمين الرقم. مع الرقم الكبير 12345، لا أريد أن أخدع رأسي، دعونا نفكر في الرقم 26 من المقال عنه. لنكتب هذا الرقم في أنظمة الأرقام الثنائية والثمانية والعشرية والست عشرية. لن ننظر إلى كل خطوة تحت المجهر؛ لقد فعلنا ذلك بالفعل. دعونا ننظر إلى النتيجة.
كما ترون، في أنظمة الأرقام المختلفة، يختلف مجموع أرقام نفس الرقم. هذه النتيجة لا علاقة لها بالرياضيات. الأمر نفسه كما لو حددت مساحة المستطيل بالمتر والسنتيمترات، فستحصل على نتائج مختلفة تمامًا.
يبدو الصفر متماثلًا في جميع أنظمة الأعداد ولا يحتوي على مجموع أرقام. وهذه حجة أخرى لصالح حقيقة ذلك. سؤال لعلماء الرياضيات: كيف يكون الشيء الذي ليس رقما محددا في الرياضيات؟ ماذا، بالنسبة لعلماء الرياضيات لا يوجد شيء سوى الأرقام؟ أستطيع أن أسمح بهذا للشامان، ولكن ليس للعلماء. الواقع لا يتعلق بالأرقام فقط.
يجب اعتبار النتيجة التي تم الحصول عليها دليلاً على أن أنظمة الأرقام هي وحدات قياس للأرقام. ففي نهاية المطاف، لا يمكننا مقارنة الأرقام بوحدات قياس مختلفة. فإذا كانت نفس الأفعال مع وحدات قياس مختلفة لنفس الكمية تؤدي إلى نتائج مختلفة بعد مقارنتها، فهذا لا علاقة له بالرياضيات.
ما هي الرياضيات الحقيقية؟ يحدث هذا عندما لا تعتمد نتيجة العملية الرياضية على حجم الرقم ووحدة القياس المستخدمة وعلى من يقوم بهذا الإجراء.
أوه! أليس هذا هو مرحاض النساء؟
- شابة! هذا مختبر لدراسة قداسة النفوس غير المحبة أثناء صعودها إلى السماء! هالة في الأعلى والسهم لأعلى. ما المرحاض الآخر؟
أنثى... الهالة الموجودة في الأعلى والسهم لأسفل هما ذكران.
إذا كان هذا العمل الفني التصميمي يومض أمام عينيك عدة مرات في اليوم،
إذن ليس من المستغرب أن تجد فجأة رمزًا غريبًا في سيارتك:
أنا شخصياً أبذل جهداً لرؤية سالب أربع درجات في شخص يتبرز (صورة واحدة) (تركيبة من عدة صور: علامة الطرح، الرقم أربعة، تعيين الدرجات). ولا أعتقد أن هذه الفتاة حمقاء ولا تعرف الفيزياء. لديها فقط صورة نمطية قوية لإدراك الصور الرسومية. وعلماء الرياضيات يعلموننا هذا طوال الوقت. هنا مثال.
1A ليس "ناقص أربع درجات" أو "واحد أ". هذا هو "رجل التغوّط" أو الرقم "ستة وعشرون" بالتدوين السداسي العشري. هؤلاء الأشخاص الذين يعملون باستمرار في نظام الأرقام هذا يدركون تلقائيًا الرقم والحرف كرمز رسومي واحد.
جدول قيم الدوال المثلثية
يتم تجميع جدول قيم الدوال المثلثية للزوايا 0 و30 و45 و60 و90 و180 و270 و360 درجة وقيم الزوايا المقابلة بالراديان. من بين الدوال المثلثية، يوضح الجدول الجيب وجيب التمام والظل وظل التمام والقاطع وقاطع التمام. ولتسهيل حل الأمثلة المدرسية، يتم كتابة قيم الدوال المثلثية في الجدول على شكل كسر مع الحفاظ على علامات استخراج الجذر التربيعي للأعداد، مما يساعد في كثير من الأحيان على تقليل التعبيرات الرياضية المعقدة. بالنسبة للظل وظل التمام، لا يمكن تحديد قيم بعض الزوايا. بالنسبة لقيم الظل وظل التمام لهذه الزوايا، توجد شرطة في جدول قيم الدوال المثلثية. ومن المقبول عمومًا أن ظل وظل التمام لهذه الزوايا يساوي اللانهاية. توجد في صفحة منفصلة صيغ لتقليل الدوال المثلثية.
يوضح جدول قيم دالة الجيب المثلثية قيم الزوايا التالية: sin 0، sin 30، sin 45، sin 60، sin 90، sin 180، sin 270، sin 360 بالدرجات، وهو ما يتوافق مع الخطيئة 0 بي، الخطيئة بي / 6، الخطيئة بي / 4، الخطيئة بي / 3، الخطيئة بي / 2، الخطيئة بي، الخطيئة 3 بي / 2، الخطيئة 2 بي في راديان قياس الزوايا. الجدول المدرسي للجيوب.
بالنسبة لدالة جيب التمام المثلثية، يوضح الجدول قيم الزوايا التالية: cos 0، cos 30، cos 45، cos 60، cos 90، cos 180، cos 270، cos 360 بالدرجات، وهو ما يتوافق مع cos 0 pi ، cos pi على 6، cos pi على 4، cos pi على 3، cos pi على 2، cos pi، cos 3 pi على 2، cos 2 pi بقياس راديان للزوايا. الجدول المدرسي لجيب التمام.
يعطي الجدول المثلثي لدالة الظل المثلثية قيمًا للزوايا التالية: tg 0، tg 30، tg 45، tg 60، tg 180، tg 360 في قياس الدرجة، وهو ما يتوافق مع tg 0 pi، tg pi/6، tg pi/4، tg pi/3، tg pi، tg 2 pi في قياس راديان للزوايا. لم يتم تعريف القيم التالية لدوال الظل المثلثية tan 90، tan 270، tan pi/2، tan 3 pi/2 وتعتبر مساوية لما لا نهاية.
بالنسبة للدالة المثلثية ظل التمام في الجدول المثلثي، يتم إعطاء قيم الزوايا التالية: ctg 30، ctg 45، ctg 60، ctg 90، ctg 270 في قياس الدرجة، وهو ما يتوافق مع ctg pi/6، ctg pi/4 ، ctg pi/3، tg pi/ 2، tan 3 pi/2 بقياس راديان للزوايا. لم يتم تعريف القيم التالية لدوال ظل التمام المثلثية ctg 0، ctg 180، ctg 360، ctg 0 pi، ctg pi، ctg 2 pi وتعتبر مساوية لما لا نهاية.
يتم إعطاء قيم الدوال المثلثية القاطعة وقاطعة التمام لنفس الزوايا بالدرجات والراديان مثل الجيب وجيب التمام والظل وظل التمام.

يوضح جدول قيم الدوال المثلثية للزوايا غير القياسية قيم الجيب وجيب التمام والظل وظل التمام للزوايا بالدرجات 15، 18، 22.5، 36، 54، 67.5 72 درجة وبالراديان pi/12 ، بي/10، بي/ 8، بي/5، 3بي/8، 2بي/5 راديان. يتم التعبير عن قيم الدوال المثلثية من حيث الكسور والجذور التربيعية لتسهيل تبسيط الكسور في الأمثلة المدرسية.

ثلاثة وحوش أخرى في علم المثلثات. الأول هو ظل 1.5 درجة ونصف أو باي مقسومًا على 120. والثاني هو جيب تمام باي مقسومًا على 240، باي/240. الأطول هو جيب تمام pi مقسومًا على 17، pi/17.

تمثل الدائرة المثلثية لقيم وظائف الجيب وجيب التمام بصريًا علامات الجيب وجيب التمام اعتمادًا على حجم الزاوية. خاصة بالنسبة للشقراوات، يتم وضع خط تحت قيم جيب التمام بشرطة خضراء لتقليل الارتباك. يتم أيضًا عرض تحويل الدرجات إلى الراديان بشكل واضح جدًا عند التعبير عن الراديان بدلالة pi.

يعرض هذا الجدول المثلثي قيم الجيب وجيب التمام والظل وظل التمام للزوايا من 0 صفر إلى 90 درجة على فترات من درجة واحدة. بالنسبة للخمسة وأربعين درجة الأولى، ينبغي النظر إلى أسماء الدوال المثلثية في أعلى الجدول. يحتوي العمود الأول على الدرجات، ويتم كتابة قيم الجيب وجيب التمام والظل وظل التمام في الأعمدة الأربعة التالية.
بالنسبة للزوايا من خمسة وأربعين درجة إلى تسعين درجة، تكتب أسماء الدوال المثلثية في أسفل الجدول. يحتوي العمود الأخير على درجات جيب التمام، وجيب التمام، وظل التمام، وظلال التمام مكتوبة في الأعمدة الأربعة السابقة. يجب الحذر لأن أسماء الدوال المثلثية الموجودة أسفل الجدول المثلثي تختلف عن الأسماء الموجودة أعلى الجدول. يتم تبادل الجيوب وجيب التمام، تمامًا مثل الظل وظل التمام. ويرجع ذلك إلى تماثل قيم الدوال المثلثية.

تظهر علامات الدوال المثلثية في الشكل أعلاه. جيب لديه قيم موجبة من 0 إلى 180 درجة، أو 0 إلى باي. جيب لديه قيم سلبية من 180 إلى 360 درجة أو من pi إلى 2 pi. تكون قيم جيب التمام موجبة من 0 إلى 90 ومن 270 إلى 360 درجة، أو من 0 إلى 1/2 pi و3/2 إلى 2 pi. الظل و ظل التمام لهما قيم موجبة من 0 إلى 90 درجة ومن 180 إلى 270 درجة، المقابلة للقيم من 0 إلى 1/2 pi و pi إلى 3/2 pi. القيم السالبة للظل وظل التمام هي من 90 إلى 180 درجة ومن 270 إلى 360 درجة، أو من 1/2 pi إلى pi ومن 3/2 pi إلى 2 pi. عند تحديد علامات الدوال المثلثية للزوايا الأكبر من 360 درجة أو 2pi، يجب عليك استخدام خصائص دورية هذه الدوال.
الدوال المثلثية الجيب والظل وظل التمام هي دوال فردية. قيم هذه الدوال للزوايا السالبة ستكون سالبة. جيب التمام هو دالة مثلثية زوجية - قيمة جيب التمام للزاوية السالبة ستكون موجبة. يجب اتباع قواعد الإشارة عند ضرب وقسمة الدوال المثلثية.
يوضح جدول قيم دالة الجيب المثلثية قيم الزوايا التالية
وثيقةتوجد صيغ التخفيض في صفحة منفصلة حساب المثاثاتالمهام. في طاولةقيملحساب المثاثاتالمهامالتجويفمنحقيملالأتىزوايا: الخطيئة 0، الخطيئة 30، الخطيئة 45 ...
الجهاز الرياضي المقترح عبارة عن تماثل كامل لحساب التفاضل والتكامل المعقد للأعداد المفرطة التعقيد ذات الأبعاد n مع أي عدد من درجات الحرية n وهو مخصص للنمذجة الرياضية للأعداد غير الخطية
وثيقة... المهاميساوي المهامالصور. من هذه النظرية يجب، ماذا لالعثور على الإحداثيات U، V، يكفي لحساب وظيفة... الهندسة؛ متعدد الأطراف المهام(نظائرها متعددة الأبعاد ثنائية الأبعاد حساب المثاثاتالمهام)، خصائصهم، الجداولوالتطبيق؛ ...
-
سنبدأ دراستنا لعلم المثلثات بالمثلث القائم الزاوية. دعونا نحدد ما هو الجيب وجيب التمام، وكذلك الظل وظل التمام لزاوية حادة. هذه هي أساسيات علم المثلثات.
دعونا نتذكر ذلك زاوية مستقيمةهي زاوية تساوي 90 درجة. وبعبارة أخرى، نصف زاوية منعطفة.
زاوية حادة- أقل من 90 درجة.
زاوية منفرجة- أكبر من 90 درجة. فيما يتعلق بهذه الزاوية، فإن "المنفرجة" ليست إهانة، ولكنها مصطلح رياضي :-)
لنرسم مثلثًا قائمًا. عادة ما يتم الإشارة إلى الزاوية اليمنى بواسطة . يرجى ملاحظة أن الجانب المقابل للزاوية يُشار إليه بالحرف نفسه، ولكنه صغير فقط. وبالتالي، يتم تعيين الجانب المقابل للزاوية A .
يُشار إلى الزاوية بالحرف اليوناني المقابل.

الوترللمثلث القائم هو الضلع المقابل للزاوية القائمة.
الساقين- الجوانب المتقابلة بزوايا حادة.
تسمى الساق الواقعة مقابل الزاوية عكس(بالنسبة للزاوية). وتسمى الساق الأخرى التي تقع على أحد جانبي الزاوية مجاور.
التجويفالزاوية الحادة في المثلث القائم هي نسبة الضلع المقابل للوتر:
جيب التمامالزاوية الحادة في المثلث الأيمن - نسبة الساق المجاورة إلى الوتر:
الظلالزاوية الحادة في المثلث القائم - نسبة الضلع المقابل إلى الضلع المجاور:
تعريف آخر (معادل): ظل الزاوية الحادة هو نسبة جيب الزاوية إلى جيب تمامها:
ظل التمامالزاوية الحادة في المثلث الأيمن - نسبة الجانب المجاور إلى المقابل (أو، وهي نفسها، نسبة جيب التمام إلى الجيب):
لاحظ العلاقات الأساسية للجيب وجيب التمام والظل وظل التمام أدناه. ستكون مفيدة لنا عند حل المشكلات.

دعونا نثبت بعض منهم.
حسنًا، لقد قدمنا تعريفات وكتبنا الصيغ. ولكن لماذا لا نزال بحاجة إلى الجيب وجيب التمام والظل والظل؟
نحن نعرف ذلك مجموع زوايا أي مثلث يساوي.
نحن نعرف العلاقة بين حفلاتمثلث قائم. وهذه هي نظرية فيثاغورس: .
اتضح أنه بمعرفة زاويتين في المثلث، يمكنك العثور على الثالثة. بمعرفة ضلعي المثلث القائم الزاوية، يمكنك العثور على الثالث. هذا يعني أن الزوايا لها نسبها الخاصة، والأضلاع لها نسبها الخاصة. ولكن ماذا يجب أن تفعل إذا كنت تعرف زاوية واحدة (باستثناء الزاوية القائمة) وضلعًا واحدًا في المثلث القائم، لكنك بحاجة إلى العثور على الجوانب الأخرى؟

وهذا ما واجهه الناس في الماضي عند عمل خرائط للمنطقة والسماء المرصعة بالنجوم. ففي النهاية، ليس من الممكن دائمًا قياس جميع أضلاع المثلث بشكل مباشر.
جيب التمام وجيب التمام والظل - يطلق عليهم أيضًا وظائف الزاوية المثلثية- إعطاء العلاقات بين حفلاتو زوايامثلث. بمعرفة الزاوية، يمكنك العثور على جميع دوالها المثلثية باستخدام جداول خاصة. وبمعرفة جيب التمام وجيب التمام وظلال زوايا المثلث وأحد أضلاعه، يمكنك إيجاد الباقي.
سنقوم أيضًا برسم جدول لقيم الجيب وجيب التمام والظل وظل التمام للزوايا "الجيدة" من إلى.
يرجى ملاحظة الشرطتين الأحمرتين في الجدول. عند قيم الزاوية المناسبة، لا يوجد ظل وظل التمام.
دعونا نلقي نظرة على العديد من مسائل علم المثلثات من بنك مهام FIPI.
1. في المثلث، الزاوية هي . يجد .
يتم حل المشكلة في أربع ثوان.
بسبب ال ، .
2. في المثلث تكون الزاوية , . يجد .

دعونا نجدها باستخدام نظرية فيثاغورس.
حلت المشكلة.
غالبًا ما توجد في المشكلات مثلثات بزوايا أو بزوايا و. حفظ النسب الأساسية لهم عن ظهر قلب!

بالنسبة للمثلث ذو الزوايا والساق المقابلة للزاوية تساوي نصف الوتر.
مثلث ذو زوايا وهو متساوي الساقين. فيه يكون الوتر أكبر من الساق مرات.
لقد بحثنا في مسائل حل المثلثات القائمة الزاوية، أي إيجاد جوانب أو زوايا مجهولة. ولكن هذا ليس كل شيء! هناك العديد من المشكلات في اختبار الدولة الموحدة في الرياضيات التي تتضمن جيب التمام أو جيب التمام أو الظل أو ظل التمام لزاوية خارجية للمثلث. المزيد عن هذا في المقالة التالية.









