أقراص، حقن

قاعدة إيجاد إحداثيات الفرق بين متجهين. إضافة المتجهات

حسنًا، عليك أولاً أن تفهم مفهومًا مثل تأجيل المتجه من نقطة معينة.

التعريف 1

إذا كانت النقطة $A$ هي بداية أي متجه $\overrightarrow(a)$، فيقال إن المتجه $\overrightarrow(a)$ قد تأخر من النقطة $A$ (الشكل 1).

الشكل 1. $\overrightarrow(a)$ مرسومة من النقطة $A$

دعونا نقدم النظرية التالية:

النظرية 1

من أي نقطة $K$ يمكن رسم متجه $\overrightarrow(a)$، علاوة على ذلك، واحد فقط.

دليل.

وجود:هناك حالتان يجب مراعاتهما هنا:

المتجه $\overrightarrow(a)$ هو صفر.

في هذه الحالة، من الواضح أن المتجه المطلوب هو المتجه $\overrightarrow(KK)$.

المتجه $\overrightarrow(a)$ ليس صفرًا.

دعونا نشير بالنقطة $A$ إلى بداية المتجه $\overrightarrow(a)$، وبالنقطة $B$ نهاية المتجه $\overrightarrow(a)$. دعونا نرسم خطًا مستقيمًا $b$ عبر النقطة $K$ موازيًا للمتجه $\overrightarrow(a)$. دعونا نرسم القطع $\left|KL\right|=|AB|$ و$\left|KM\right|=|AB|$ على هذا الخط. خذ بعين الاعتبار المتجهين $\overrightarrow(KL)$ و$\overrightarrow(KM)$. من بين هذين المتجهين، سيكون المتجه المطلوب هو المتجه المشترك مع المتجه $\overrightarrow(a)$ (الشكل 2)

الشكل 2. رسم توضيحي للنظرية 1

التفرد:التفرد يتبع مباشرة من البناء الذي تم تنفيذه في نقطة "الوجود".

لقد تم إثبات النظرية.

طرح المتجهات. القاعدة الأولى

دعونا نعطي المتجهين $\overrightarrow(a)$ و$\overrightarrow(b)$.

التعريف 2

الفرق بين المتجهين $\overrightarrow(a)$ و $\overrightarrow(b)$ هو المتجه $\overrightarrow(c)$ والذي، عند إضافته إلى المتجه $\overrightarrow(b)$، يعطي المتجه $\ overrightarrow(a)$ ، هذا هو

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

تعيين:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

دعونا نفكر في بناء الفرق بين متجهين باستخدام المشكلة.

مثال 1

دع المتجهين $\overrightarrow(a)$ و $\overrightarrow(b)$ معطى. أنشئ المتجه $\overrightarrow(a)-\overrightarrow(b)$.

حل.

لنقم بإنشاء نقطة عشوائية $O$ ونرسم المتجهات $\overrightarrow(OA)=\overrightarrow(a)$ و $\overrightarrow(OB)=\overrightarrow(b)$ منها. من خلال ربط النقطة $B$ بالنقطة $A$، نحصل على المتجه $\overrightarrow(BA)$ (الشكل 3).

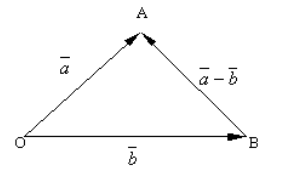
الشكل 3. الفرق بين ناقلين

وباستخدام قاعدة المثلث لإيجاد مجموع متجهين، نلاحظ ذلك

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

ومن التعريف 2، حصلنا على ذلك

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

إجابة:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

من هذه المسألة نحصل على القاعدة التالية لإيجاد الفرق بين متجهين. للعثور على الفرق $\overrightarrow(a)-\overrightarrow(b)$ تحتاج إلى رسم المتجهات $\overrightarrow(OA)=\overrightarrow(a)$ و $\overrightarrow(OB)=\overrightarrow(b) من نقطة عشوائية $O$ )$ وقم بتوصيل نهاية المتجه الثاني بنهاية المتجه الأول.

طرح المتجهات. القاعدة الثانية

دعونا نتذكر المفهوم التالي الذي نحتاجه.

التعريف 3

يسمى المتجه $\overrightarrow(a_1)$ تعسفيًا للمتجه $\overrightarrow(a)$ إذا كانت هذه المتجهات متقابلة في الاتجاه ولها نفس الطول.

تعيين:المتجه $(-\overrightarrow(a))$ هو عكس المتجه $\overrightarrow(a)$.

لكي نقدم القاعدة الثانية للفرق بين متجهين، علينا أولًا تقديم وإثبات النظرية التالية.

النظرية 2

بالنسبة لأي متجهين $\overrightarrow(a)$ و $\overrightarrow(b)$ فإن المساواة التالية تحمل:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

دليل.

حسب التعريف 2، لدينا

نضيف المتجه $\left(-\overrightarrow(b)\right)$ إلى كلا الجزأين، ونحصل على ذلك

بما أن المتجهين $\overrightarrow(b)$ و $\left(-\overrightarrow(b)\right)$ متقابلان، فإن $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ السهم الأيمن (0)$. لدينا

لقد تم إثبات النظرية.

من هذه النظرية نحصل على القاعدة التالية للفرق بين متجهين: للعثور على الفرق $\overrightarrow(a)-\overrightarrow(b)$، نحتاج إلى رسم المتجه $\overrightarrow(OA)=\overrightarrow(a) )$ من نقطة اختيارية $O$، ثم من النقطة الناتجة $A$، ارسم المتجه $\overrightarrow(AB)=-\overrightarrow(b)$ وقم بتوصيل بداية المتجه الأول بنهاية المتجه المتجه الثاني.

مثال على مشكلة حول مفهوم اختلاف المتجهات

مثال 2

دعونا نعطي متوازي الأضلاع $ADCD$ الذي تتقاطع أقطاره عند النقطة $O$. $\overrightarrow(AB)=\overrightarrow(a)$، $\overrightarrow(AD)=\overrightarrow(b)$ (الشكل 4). عبر عن المتجهات التالية من خلال المتجهين $\overrightarrow(a)$ و$\overrightarrow(b)$:

أ) $\overrightarrow(DC)+\overrightarrow(CB)$

ب) $\overrightarrow(BO)-\overrightarrow(OC)$

الشكل 4. متوازي الأضلاع

حل.

أ) نقوم بإجراء عملية الجمع وفقا لقاعدة المثلث، نحصل عليها

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

من القاعدة الأولى للفرق بين متجهين، نحصل على

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

ب) بما أن $\overrightarrow(OC)=\overrightarrow(AO)$، فقد حصلنا على ذلك

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

حسب النظرية 2، لدينا

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

باستخدام قاعدة المثلث، وصلنا أخيرًا

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

مجموع المتجهات. طول المتجهات. أصدقائي الأعزاء، ضمن أنواع الامتحانات هناك مجموعة من المسائل المتعلقة بالمتجهات. المهام واسعة النطاق (من المهم معرفة الأسس النظرية). يتم حل معظمها شفويا. تتعلق الأسئلة بإيجاد طول المتجه ومجموع (فرق) المتجهات وحاصل الضرب القياسي. هناك أيضًا العديد من المهام التي يلزم فيها تنفيذ إجراءات بإحداثيات المتجهات.

النظرية المحيطة بموضوع المتجهات ليست معقدة، ويجب فهمها جيدًا. في هذه المقالة سوف نقوم بتحليل المسائل المتعلقة بإيجاد طول المتجه، وكذلك مجموع (الفرق) للمتجهات. بعض النقاط النظرية:

مفهوم المتجهات

المتجه هو قطعة موجهة.

جميع المتجهات التي لها نفس الاتجاه ومتساوية في الطول متساوية.

*جميع المتجهات الأربعة المذكورة أعلاه متساوية!

أي أننا إذا حركنا المتجه المعطى لنا باستخدام النقل المتوازي، فسنحصل دائمًا على متجه يساوي المتجه الأصلي. وبالتالي، يمكن أن يكون هناك عدد لا حصر له من المتجهات المتساوية.

تدوين المتجهات

يمكن الإشارة إلى المتجه بالأحرف اللاتينية الكبيرة، على سبيل المثال:

باستخدام هذا النوع من التدوين، يتم أولاً كتابة الحرف الذي يشير إلى بداية المتجه، ثم الحرف الذي يشير إلى نهاية المتجه.

يُشار إلى المتجه الآخر بحرف واحد من الأبجدية اللاتينية (الحرف الكبير):

التعيين بدون أسهم ممكن أيضًا:

مجموع المتجهين AB و BC سيكون المتجه AC.
يتم كتابته على النحو التالي AB + BC = AC.

تسمى هذه القاعدة - حكم المثلث.

أي أنه إذا كان لدينا متجهان - دعنا نسميهما بشكل تقليدي (1) و(2)، وكانت نهاية المتجه (1) تتطابق مع بداية المتجه (2)، فإن مجموع هذه المتجهات سيكون متجهًا البداية تتزامن مع بداية المتجه (1)، والنهاية تتزامن مع نهاية المتجه (2).

الخلاصة: إذا كان لدينا متجهان على المستوى، فيمكننا دائمًا إيجاد مجموعهما. باستخدام الترجمة المتوازية، يمكنك نقل أي من هذه المتجهات وربط بدايتها بنهاية أخرى. على سبيل المثال:

دعونا نحرك المتجه ب، أو بعبارة أخرى، دعونا نبني واحدة متساوية:

كيف يتم العثور على مجموع عدة ناقلات؟ وبنفس المبدأ:

* * *

قاعدة متوازي الأضلاع

هذه القاعدة هي نتيجة لما سبق.

بالنسبة للمتجهات ذات الأصل المشترك، يتم تمثيل مجموعها بقطر متوازي الأضلاع المبني على هذه المتجهات.

لنقم ببناء متجه يساوي المتجه ببحيث تتزامن بدايته مع نهاية المتجه أ، ويمكننا بناء متجه يكون مجموعهما:

هناك حاجة إلى معلومات أكثر أهمية لحل المشكلات.

يُشار أيضًا إلى المتجه المساوٍ للطول الأصلي، ولكنه موجه بشكل معاكس، ولكن له علامة معاكسة:

هذه المعلومات مفيدة للغاية في حل المسائل التي تتضمن إيجاد الفرق بين المتجهات. كما ترون، الفرق المتجه هو نفس المجموع في شكل معدل.

لنفترض أن هناك متجهين، أوجد الفرق بينهما:

لقد أنشأنا متجهًا معاكسًا للمتجه b، وأوجدنا الفرق.

إحداثيات المتجهات

للعثور على إحداثيات المتجه، تحتاج إلى طرح الإحداثيات المقابلة للبداية من إحداثيات النهاية:

أي أن إحداثيات المتجهات هي زوج من الأرقام.

لو

وإحداثيات المتجهات تبدو كما يلي:

ثم ج 1 = أ 1 + ب 1 ج 2 = أ 2 + ب 2

لو

ثم ج 1 = أ 1 - ب 1 ج 2 = أ 2 - ب 2

وحدة المتجهات

معامل المتجه هو طوله، ويتم تحديده بالصيغة:

صيغة تحديد طول المتجه إذا كانت إحداثيات بدايته ونهايته معروفة:

دعونا نفكر في المهام:

ضلعا المستطيل ABCD يساويان 6 و8. يتقاطع القطران عند النقطة O. أوجد طول الفرق بين المتجهين AO وBO.

لنجد المتجه الذي سيكون نتيجة AO–VO:

AO –VO =AO +(–VO )=AB

وهذا هو، الفرق بين المتجهات AO و سيكون VO متجهًا أ.ب. وطوله ثمانية.

أقطار المعين ا ب ت ثيساويان 12 و16. أوجد طول المتجه AB + AD.

دعونا نجد المتجه الذي سيكون مجموع المتجهين AD و AB BC يساوي المتجه AD. إذن AB + AD = AB + BC = AC

AC هو طول قطر المعين تكييف، وهو يساوي 16.

أقطار المعين ABCD تتقاطع عند هذه النقطة ياوهما يساويان 12 و16. أوجد طول المتجه AO + BO.

دعونا نجد المتجه الذي سيكون مجموع المتجهين AO و VO VO يساوي المتجه OD، مما يعني

AD هو طول ضلع المعين. تتلخص المشكلة في إيجاد الوتر في المثلث القائم الزاوية AOD. دعونا نحسب الساقين:

وفقا لنظرية فيثاغورس:

قطرا المعين ABCD يتقاطعان عند النقطة O ويساويان 12 و16. أوجد طول المتجه AO – BO.

لنجد المتجه الذي سيكون نتيجة AO–VO:

AB هو طول ضلع المعين. تكمن المشكلة في إيجاد الوتر AB في المثلث القائم AOB. دعونا نحسب الساقين:

وفقا لنظرية فيثاغورس:

أضلاع المثلث المنتظم ABC تساوي 3.

أوجد طول المتجه AB –AC.

دعونا نجد نتيجة الفرق المتجه:

CB يساوي ثلاثة، لأن الشرط ينص على أن المثلث متساوي الأضلاع وأضلاعه تساوي 3.

27663. أوجد طول المتجه أ (6؛8).

27664. أوجد مربع طول المتجه AB.

يمكن اعتبار المتجه $\overrightarrow(AB)$ بمثابة حركة نقطة من الموضع $A$ (بداية الحركة) إلى الموضع $B$ (نهاية الحركة). أي أن مسار الحركة في هذه الحالة ليس مهما، فقط البداية والنهاية مهمتان!

$\blacktriangleright$ يكون المتجهان على خط واحد إذا كانا يقعان على نفس الخط أو على خطين متوازيين.
وبخلاف ذلك، تسمى المتجهات غير خطية.

$\blacktriangleright$ يطلق على متجهين على خط واحد اسم متجهين مشتركين إذا تطابقت اتجاهاتهما.
إذا كانت اتجاهاتهم متضادة، فيطلق عليهم اتجاه معاكس.

قواعد إضافة المتجهات الخطية:

شارك في الإخراج نهايةأولاً. ثم يكون مجموعهم متجهًا، بدايته تتزامن مع بداية المتجه الأول، ونهايته مع نهاية المتجه الثاني (الشكل 1).

$\blacktriangleright$ لإضافة اثنين موجهة بشكل معاكسالمتجه، يمكننا تأجيل المتجه الثاني من بدأتأولاً. ثم يكون مجموعهم متجهًا، تتزامن بدايته مع بداية كلا المتجهين، والطول يساوي الفرق في أطوال المتجهات، ويتزامن الاتجاه مع اتجاه المتجه الأطول (الشكل 2).

قواعد إضافة المتجهات غير الخطية $\overrightarrow (a)$ و $\overrightarrow(b)$ :

$\blacktriangleright$ قاعدة المثلث (الشكل 3).

من الضروري وضع المتجه $\overrightarrow (b)$ جانبًا من نهاية المتجه $\overrightarrow (a)$. إذن المجموع هو متجه، بدايته تتزامن مع بداية المتجه $\overrightarrow (a)$ ، والنهاية مع نهاية المتجه $\overrightarrow (b)$ .

$\blacktriangleright$ قاعدة متوازي الأضلاع (الشكل 4).

من الضروري وضع المتجه $\overrightarrow (b)$ جانبًا من بداية المتجه $\overrightarrow (a)$. ثم المبلغ $\overrightarrow (a)+\overrightarrow (b)$- متجه يتطابق مع قطر متوازي الأضلاع المبني على المتجهين $\overrightarrow (a)$ و$\overrightarrow (b)$ (تتزامن بدايته مع بداية كلا المتجهين).

$\blacktriangleright$ لإيجاد الفرق بين متجهين $\overrightarrow (a)-\overrightarrow(b)$، فأنت بحاجة إلى العثور على مجموع المتجهات $\overrightarrow (a)$ و $-\overrightarrow(b)$ : $\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))$(الشكل 5).

المهمة 1 #2638

مستوى المهمة: أصعب من امتحان الدولة الموحدة

إذا كان لدينا مثلث قائم الزاوية $ABC$ بزاوية قائمة $A$، فإن النقطة $O$ هي مركز الدائرة المحيطة بهذا المثلث. إحداثيات المتجهات $\overrightarrow(AB)=\(1;1$\), $\overrightarrow(AC)=\(-1;1$\). أوجد مجموع إحداثيات المتجه $\overrightarrow(OC)$ .

لأن إذا كان المثلث $ABC$ مستطيلاً، فإن مركز الدائرة المحصورة يقع في منتصف الوتر، أي. $O$ هو منتصف $BC$ .

لاحظ أن $\overrightarrow(BC)=\overrightarrow(AC)-\overrightarrow(AB)$، لذلك، $\overrightarrow(BC)=\(-1-1;1-1$=$-2;0$\).

لأن $\overrightarrow(OC)=\dfrac12 \overrightarrow(BC)$، الذي - التي $\overrightarrow(OC)=\(-1;0$\).

هذا يعني أن مجموع إحداثيات المتجه $\overrightarrow(OC)$ يساوي $-1+0=-1$ .

الجواب: -1

المهمة 2 #674

مستوى المهمة: أصعب من امتحان الدولة الموحدة

$\overrightarrow$ - شكل رباعي على جوانبه المتجهات $\overrightarrow(AB)$ , $\overrightarrow(BC)$ , $\overrightarrow(CD)$ , $\overrightarrow( دا) $ . أوجد طول المتجه $\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA)$.

$\overrightarrow(AB) + \overrightarrow(BC) = \overrightarrow(AC)$, $\overrightarrow(AC) + \overrightarrow(CD) = \overrightarrow(AD)$، ثم
$\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA) = \overrightarrow(AC) + \overrightarrow(CD) + \overrightarrow(DA)= \overrightarrow(AD) + \overrightarrow(DA) = \overrightarrow(AD) - \overrightarrow(AD) = \vec(0)$.
طول المتجه الفارغ يساوي $0$ .

يمكن إذن اعتبار المتجه بمثابة إزاحة $\overrightarrow(AB) + \overrightarrow(BC)$- الانتقال من $A$ إلى $B$ ثم من $B$ إلى $C$ - في النهاية هذا هو الانتقال من $A$ إلى $C$ .

وبهذا التفسير يتبين أن $\overrightarrow(AB) + \overrightarrow(BC) + \overrightarrow(CD) + \overrightarrow(DA) = \vec(0)$، لأننا في النهاية انتقلنا هنا من النقطة $A$ إلى النقطة $A$، أي أن طول هذه الحركة هو $0$، مما يعني أن متجه هذه الحركة نفسها هو \ (\vec(0)\) .

الجواب: 0

المهمة 3 #1805

مستوى المهمة: أصعب من امتحان الدولة الموحدة

نظرا لمتوازي الأضلاع $ABCD$ . يتقاطع القطران $AC$ و $BD$ عند النقطة $O$ . دعونا، إذن $\overrightarrow(OA) = x\cdot\vec(a) + y\cdot\vec(b)$

\[\overrightarrow(OA) = \frac(1)(2)\overrightarrow(CA) = \frac(1)(2)(\overrightarrow(CB) + \overrightarrow(BA)) = \frac(1)( 2)(\overrightarrow(DA) + \overrightarrow(BA)) = \frac(1)(2)(-\vec(b) - \vec(a)) = - \frac(1)(2)\vec (أ) - \frac(1)(2)\vec(b)\]$\Rightarrow$ $x = - \frac(1)(2)$ , $y = - \frac(1)(2)$ $\Rightarrow$ $x + y = - 1$ .

الجواب: -1

المهمة 4 #1806

مستوى المهمة: أصعب من امتحان الدولة الموحدة

نظرا لمتوازي الأضلاع $ABCD$ . تقع النقطتان $K$ و $L$ على الجانبين $BC$ و $CD$، على التوالي، و $BK:KC = 3:1$ و $L$ هي منتصف \ (CD\) . يترك $\overrightarrow(AB) = \vec(a)$, $\overrightarrow(AD) = \vec(b)$، ثم $\overrightarrow(KL) = x\cdot\vec(a) + y\cdot\vec(b)$، حيث $x$ و $y$ عبارة عن بعض الأرقام. أوجد الرقم الذي يساوي $x + y$ .

\[\overrightarrow(KL) = \overrightarrow(KC) + \overrightarrow(CL) = \frac(1)(4)\overrightarrow(BC) + \frac(1)(2)\overrightarrow(CD) = \frac (1)(4)\overrightarrow(AD) + \frac(1)(2)\overrightarrow(BA) = \frac(1)(4)\vec(b) - \frac(1)(2)\vec (أ)\]$\Rightarrow$ $x = -\frac(1)(2)$ , $y = \frac(1)(4)$ $\Rightarrow$ $x + y = -0 ،25$ .

الجواب: -0.25

المهمة 5 #1807

مستوى المهمة: أصعب من امتحان الدولة الموحدة

نظرا لمتوازي الأضلاع $ABCD$ . تقع النقطتان $M$ و$N$ على الجانبين $AD$ و$BC$، على التوالي، مع $AM:MD = 2:3$ و$BN:NC = 3: 1$ . يترك $\overrightarrow(AB) = \vec(a)$, $\overrightarrow(AD) = \vec(b)$، ثم $\overrightarrow(MN) = x\cdot\vec(a) + y\cdot\vec(b)$

\[\overrightarrow(MN) = \overrightarrow(MA) + \overrightarrow(AB) + \overrightarrow(BN) = \frac(2)(5)\overrightarrow(DA) + \overrightarrow(AB) + \frac(3) )(4)\overrightarrow(BC) = - \frac(2)(5)\overrightarrow(AD) + \overrightarrow(AB) + \frac(3)(4)\overrightarrow(BC) = -\frac(2) )(5)\vec(b) + \vec(a) + \frac(3)(4)\vec(b) = \vec(a) + \frac(7)(20)\vec(b)\ ]$\Rightarrow$ $x = 1$ , $y = \frac(7)(20)$ $\Rightarrow$ $x\cdot y = 0.35$ .

الجواب: 0.35

المهمة 6 #1808

مستوى المهمة: أصعب من امتحان الدولة الموحدة

نظرا لمتوازي الأضلاع $ABCD$ . تقع النقطة $P$ على القطر $BD$، وتقع النقطة $Q$ على الجانب $CD$، و $BP:PD = 4:1$، و $ CQ:QD = 1:9$ . يترك $\overrightarrow(AB) = \vec(a)$, $\overrightarrow(AD) = \vec(b)$، ثم $\overrightarrow(PQ) = x\cdot\vec(a) + y\cdot\vec(b)$، حيث $x$ و $y$ عبارة عن بعض الأرقام. ابحث عن الرقم الذي يساوي $x\cdot y$ .

\[\begin(gathered) \overrightarrow(PQ) = \overrightarrow(PD) + \overrightarrow(DQ) = \frac(1)(5)\overrightarrow(BD) + \frac(9)(10)\overrightarrow( DC) = \frac(1)(5)(\overrightarrow(BC) + \overrightarrow(CD)) + \frac(9)(10)\overrightarrow(AB) =\\ = \frac(1)(5) (\overrightarrow(AD) + \overrightarrow(BA)) + \frac(9)(10)\overrightarrow(AB) = \frac(1)(5)(\overrightarrow(AD) - \overrightarrow(AB)) + \frac(9)(10)\overrightarrow(AB) = \frac(1)(5)\overrightarrow(AD) + \frac(7)(10)\overrightarrow(AB) = \frac(1)(5) \vec(b) + \frac(7)(10)\vec(a)\end(مجمع)\]

$\Rightarrow$ $x = \frac(7)(10)$ , $y = \frac(1)(5)$ $\Rightarrow$ $x\cdot y = 0, 14$ . و$ABCO$ - متوازي الأضلاع؛ $AF \parallel BE$ و $ABOF$ – متوازي الأضلاع $\Rightarrow$ \[\overrightarrow(BC) = \overrightarrow(AO) = \overrightarrow(AB) + \overrightarrow(BO) = \overrightarrow(AB) + \overrightarrow(AF) = \vec(a) + \vec(b)\ ]$\Rightarrow$ $x = 1$ , $y = 1$ $\Rightarrow$ $x + y = 2$ .

الجواب: 2

طلاب المدارس الثانوية الذين يستعدون لإجراء امتحان الدولة الموحدة في الرياضيات وفي الوقت نفسه يعتمدون على الحصول على درجات جيدة، يجب عليهم بالتأكيد تكرار موضوع "قواعد إضافة وطرح عدة ناقلات". وكما يتبين من سنوات عديدة من الممارسة، يتم تضمين هذه المهام في اختبار الشهادة كل عام. إذا واجه الخريج صعوبات في مسائل من قسم "الهندسة المستوية"، على سبيل المثال، والتي من الضروري فيها تطبيق قواعد جمع وطرح المتجهات، فيجب عليه بالتأكيد تكرار المادة أو إعادة فهمها من أجل اجتياز المادة بنجاح. امتحان الدولة الموحدة.

يقدم مشروع شكولكوفو التعليمي نهجا جديدا للتحضير لاختبار الشهادة. تم تصميم مواردنا بطريقة تمكن الطلاب من تحديد الأقسام الأكثر صعوبة لأنفسهم وسد الفجوات في المعرفة. قام متخصصو شكولكوفو بإعداد وتنظيم جميع المواد اللازمة للتحضير لاجتياز اختبار الشهادة.

للتأكد من أن مشاكل الاستخدام التي تحتاج فيها إلى تطبيق قواعد إضافة وطرح متجهين لا تسبب صعوبات، نوصي أولاً بتحسين المفاهيم الأساسية. سيتمكن الطلاب من العثور على هذه المادة في قسم "المعلومات النظرية".

إذا كنت تتذكر بالفعل قاعدة طرح المتجهات والتعريفات الأساسية حول هذا الموضوع، نقترح عليك تعزيز معرفتك من خلال إكمال التمارين المناسبة، والتي تم اختيارها من قبل المتخصصين في بوابة شكولكوفو التعليمية. لكل مشكلة، يقدم الموقع خوارزمية حل ويعطي الإجابة الصحيحة. يقدم موضوع "قواعد إضافة المتجهات" تمارين متنوعة؛ بعد إكمال مهمتين أو ثلاث مهمات سهلة نسبيًا، يمكن للطلاب الانتقال بالتتابع إلى مهام أكثر تعقيدًا.

يتمتع تلاميذ المدارس بفرصة صقل مهاراتهم في مثل هذه المهام، على سبيل المثال، عبر الإنترنت، أثناء تواجدهم في موسكو أو أي مدينة أخرى في روسيا. إذا لزم الأمر، يمكن حفظ المهمة في قسم "المفضلة". بفضل هذا، يمكنك العثور بسرعة على أمثلة مثيرة للاهتمام ومناقشة الخوارزميات للعثور على الإجابة الصحيحة مع معلمك.

تعريف

تتم إضافة المتجهات وفقًا لـ حكم المثلث.

كمية اثنين من المتجهاتيسمون مثل هذا المتجه الثالث، الذي تتزامن بدايته مع البداية، ونهايته مع النهاية، بشرط أن تتطابق نهاية المتجه وبداية المتجه (الشكل 1).

للإضافة ثلاثة أبعادتنطبق أيضًا قاعدة متوازي الأضلاع.

تعريف

قاعدة متوازي الأضلاع- إذا تم إحضار متجهين غير خطيين إلى أصل مشترك، فإن المتجه يتزامن مع قطري متوازي الأضلاع المبني على المتجهات (الشكل 2). علاوة على ذلك، فإن بداية المتجه تتزامن مع بداية المتجهات المعطاة.

تعريف

يسمى المتجه ناقلات المعاكسإلى المتجه إذا كان على استطرادالمتجه يساويه في الطول ولكنه موجه في الاتجاه المعاكس للمتجه.

تتميز عملية إضافة المتجهات بالخصائص التالية:

تعريف

بالفارق ثلاثة أبعادويسمى متجهًا بحيث يتحقق الشرط: (الشكل 3).

ضرب المتجه بعدد

تعريف

العمل المتجه لكل رقمهو ناقل يحقق الشروط:

خصائص ضرب المتجه بعدد:

هنا و هي متجهات عشوائية، وأرقام عشوائية.

الفضاء الإقليدي(أيضًا الفضاء الإقليدي) - بالمعنى الأصلي الفضاء الذي وصفت خصائصه البديهيات الهندسة الإقليدية. في هذه الحالة، من المفترض أن الفضاء لديه البعديساوي 3.

بالمعنى الحديث، وبمعنى أكثر عمومية، يمكن أن يعني أحد الأشياء المتشابهة والمرتبطة ارتباطًا وثيقًا: محدودة الأبعاد حقيقي مساحة المتجهاتمع تقديم تعريف إيجابي عليه المنتج العددي، أو الفضاء المتري، المقابلة لمثل هذه المساحة المتجهة. في هذه المقالة، سيتم اتخاذ التعريف الأول كنقطة انطلاق.

غالبًا ما يُشار إلى الفضاء الإقليدي الأبعاد أيضًا بالترميز (إذا كان واضحًا من السياق أن الفضاء له بنية إقليدية).

لتعريف الفضاء الإقليدي، من الأسهل اعتباره المفهوم الأساسي المنتج نقطة. يتم تعريف الفضاء المتجه الإقليدي بأنه محدودة الأبعاد مساحة المتجهاتفوق مجال أرقام حقيقية، والتي يتم إعطاءها على ناقلاتها دالة ذات قيمة حقيقيةلها الخصائص الثلاثة التالية:

مساحة أفينيةيُطلق على الفضاء المتجه المطابق لمثل هذا الفضاء المتجه اسم الفضاء الإقليدي، أو ببساطة الفضاء الإقليدي .

مثال على الفضاء الإقليدي هو الفضاء الإحداثي الذي يتكون من كل ما هو ممكن ن-أعداد حقيقية، المنتج العددي الذي يتم تحديده بواسطة الصيغة

إحداثيات الأساس والمتجه

أساس (اليونانية القديمةβασις، أساس) - مجموعة من هذا القبيل ثلاثة أبعادالخامس مساحة المتجهاتأن أي متجه لهذا الفضاء يمكن تمثيله بشكل فريد في النموذج تركيبة خطيةالمتجهات من هذه المجموعة - ناقلات الأساس.

وفي الحالة التي يكون فيها الأساس لا نهائيا، فإن مفهوم "التركيب الخطي" يحتاج إلى توضيح. وهذا يؤدي إلى نوعين رئيسيين من التعريف:

أساس هامل، الذي يأخذ تعريفه بعين الاعتبار المجموعات الخطية المحدودة فقط. يستخدم أساس هامل بشكل رئيسي في الجبر المجرد (على وجه الخصوص، الجبر الخطي).

أساس شودر، والذي يأخذ تعريفه أيضًا في الاعتبار مجموعات خطية لا حصر لها، أي التوسع في صفوف. يستخدم هذا التعريف بشكل رئيسي في التحليل الوظيفي، على وجه الخصوص مساحة هيلبرت,

في الفضاءات ذات الأبعاد المحدودة، يتطابق كلا النوعين من الأساس.

إحداثيات المتجهات— معاملات الممكن الوحيد تركيبة خطية أساسي ثلاثة أبعادفي المختارة نظام الإحداثيات، يساوي هذا المتجه.

أين هي إحداثيات المتجه.

المنتج العددي.

عملية جراحية على اثنين ثلاثة أبعاد، والنتيجة هي رقم[عند النظر إلى المتجهات، غالبًا ما يتم استدعاء الأرقام العددية]، مستقل عن نظام الإحداثيات ويميز أطوال ناقلات العوامل و ركنبينهم. هذه العملية تتوافق مع الضرب طولالمتجه سعلى تنبؤالمتجه ذإلى المتجه س. عادة ما تعتبر هذه العملية تبادليو خطيلكل عامل.

المنتج العدديمتجهان يساوي مجموع منتجات الإحداثيات المقابلة لهما:

ناقلات العمل الفني

هذا طبيب كاذب, عموديالطائرة مبنية من عاملين، وهي النتيجة عملية ثنائية"الضرب ناقلات" أكثر ثلاثة أبعادفي ثلاثة أبعاد الفضاء الإقليدي. المنتج الاتجاهي ليس له خصائص التبادليةو الترابط(يكون مضاد للتبديل) وعلى عكس المنتج العددي للمتجهات، هو ناقل. تستخدم على نطاق واسع في العديد من التطبيقات الهندسية والفيزيائية. على سبيل المثال، الزخم الزاويو قوة لورنتزمكتوبة رياضيا كمنتج متجه. يعتبر الضرب الاتجاهي مفيدًا في "قياس" عمودي المتجهات - معامل الضرب الاتجاهي لمتجهين يساوي منتج معامليهما إذا كانا متعامدين، وينخفض إلى الصفر إذا كانت المتجهات متوازية أو غير متوازية.

ناقلات العمل الفنييمكن حساب متجهين باستخدام المحدد المصفوفات

قطعة مختلطة

منتج مختلط ثلاثة أبعاد -المنتج العددي المتجهعلى منتج ناقلات ثلاثة أبعادو:

في بعض الأحيان يطلق عليه المنتج العددي الثلاثيالمتجهات، على ما يبدو يرجع ذلك إلى حقيقة أن النتيجة العددية(أكثر دقة - العددية الزائفة).

المعنى الهندسي:معامل المنتج المختلط يساوي عدديا الحجم متوازي السطوح، متعلم ثلاثة أبعاد .عمل مختلطيمكن العثور على ثلاثة نواقل من خلال المحدد

الطائرة في الفضاء

طائرة - سطح جبريالطلب الأول: في نظام الإحداثيات الديكارتيةيمكن تحديد الطائرة معادلةالدرجة الأولى.

بعض الخصائص المميزة للطائرة

طائرة - سطح، تحتوي على كل منها بالكامل مباشر، ربط أي منها نقاط;

المستويان إما متوازيان أو متقاطعان في خط مستقيم.

الخط المستقيم إما أن يكون موازيا للمستوى، أو يتقاطع معه في نقطة واحدة، أو يكون على المستوى.

خطان متعامدان على نفس المستوى متوازيان مع بعضهما البعض.

طائرتان متعامدتان على نفس الخط متوازيتان مع بعضهما البعض.

على نفس المنوال شريحةو فاصلة، يمكن تسمية المستوى الذي لا يتضمن نقاطًا متطرفة بالمستوى الفاصل أو المستوى المفتوح.

المعادلة العامة (الكاملة) للطائرة

حيث و هي ثوابت، وفي نفس الوقت لا تساوي الصفر؛ الخامس المتجهاستمارة:

أين هو ناقل نصف القطر للنقطة، المتجه عمودي على الطائرة (ناقل عادي). خطوط إرشادجيب التمام المتجه:

لن يجادل أحد بأنه من المستحيل الوصول إلى وجهتك دون معرفة اتجاه السفر. في الفيزياء يسمى هذا المفهوم المتجه. حتى هذه اللحظة، كنا نتعامل مع بعض الأرقام والقيم، والتي تسمى الكميات. ويختلف المتجه عن الكمية في أنه له اتجاه.

عند العمل مع ناقل، يعملون عليه اتجاهو مقاس. يتم استدعاء المعلمة المادية بغض النظر عن الاتجاه العددية.

بصريا، يتم عرض المتجه كسهم. طول السهم هو حجم المتجه.

في الفيزياء، يتم تمثيل المتجهات بحرف كبير مع وجود سهم في الأعلى.

يمكن مقارنة المتجهات. سيكون المتجهان متساويين إذا كان لهما نفس الحجم والاتجاه.

يمكن إضافة المتجهات. المتجه الناتج هو مجموع كلا المتجهين ويحدد المسافة والاتجاه. على سبيل المثال، أنت تعيش في كييف وقررت زيارة الأصدقاء القدامى في موسكو، ومن هناك قم بزيارة حماتك الحبيبة في لفيف. إلى أي مدى ستبتعد عن منزلك أثناء زيارتك لوالدة زوجتك؟

للإجابة على هذا السؤال، عليك رسم متجه من نقطة بداية الرحلة (كييف) إلى النقطة النهائية (لفيف). يحدد المتجه الجديد نتيجة الرحلة بأكملها من البداية إلى النهاية.

المتجه أ - كييف-موسكو
ناقل ب - موسكو لفيف
فيكتور سي - كييف لفيف

ج = أ+ب، أين سي - ما تها التامةأو المتجه الناتج

لا يمكن إضافة المتجهات فحسب، بل يمكن طرحها أيضًا! للقيام بذلك، تحتاج إلى الجمع بين قواعد متجه الطرح ومتجهات الطرح وربط طرفيهما بالأسهم:

المتجه أ = ج-ب
المتجه B = C-A

دعونا نطبق شبكة الإحداثيات على المتجهات لدينا. بالنسبة للمتجه A، يمكننا القول أنه تم توجيه 5 خلايا لأعلى (قيمة المحور Y الموجبة) و3 خلايا إلى اليسار (قيمة المحور X السالبة): X=-3؛ ص = 5.

بالنسبة للمتجه B: اتجاه 4 خلايا إلى اليسار و7 خلايا إلى الأسفل: X=-4؛ ص=-7.

وبالتالي، لإضافة متجهات على طول المحورين X وY، تحتاج إلى إضافة إحداثياتها. للحصول على إحداثيات المتجه الناتج على طول المحورين X وY:

دعونا نفكر في المشكلة: تتحرك الكرة بسرعة 10 m/s على مستوى مائل طول قاعدته X = 1 m، ويقع بزاوية 30° على الأفقي. ويشترط تحديد الزمن الذي تتحرك فيه الكرة من بداية المستوى إلى نهايته.

في هذه المشكلة، السرعة هي ناقل الخامسبقوة 10 م / ث واتجاهها α = 30 درجةإلى الأفقي. لتحديد سرعة حركة الكرة على طول قاعدة المستوى المائل، نحتاج إلى تحديد المكون X لحركة الكرة، وهو عددي (له قيمة فقط، وليس اتجاه) ويشار إليه بـ VX. وبالمثل، فإن المكون Y للسرعة هو أيضًا عددي ويُشار إليه الخامس ذ. ناقل السرعة من خلال المكونات: الخامس = (الخامس س؛الخامس ذ)